Bạn cảm thấy “nhức đầu” mỗi lần phải học công thức tính diện tích khối chóp? Đừng lo, vì trong bài viết này bạn sẽ khám phá cách học thông minh giúp ghi nhớ dễ dàng mà không cần học vẹt. Không lý thuyết khô khan, không công thức rối rắm — chỉ còn lại mẹo học trực quan, dễ hiểu và hiệu quả bất ngờ. Cùng KidsUP khám phá ngay nhé!
Công thức tính diện tích khối chóp
Để tính diện tích khối chóp, chúng ta cần phân biệt rõ hai khái niệm: diện tích xung quanh và diện tích toàn phần. Mỗi loại diện tích sẽ có công thức riêng, dựa trên các yếu tố hình học đặc trưng của khối chóp.
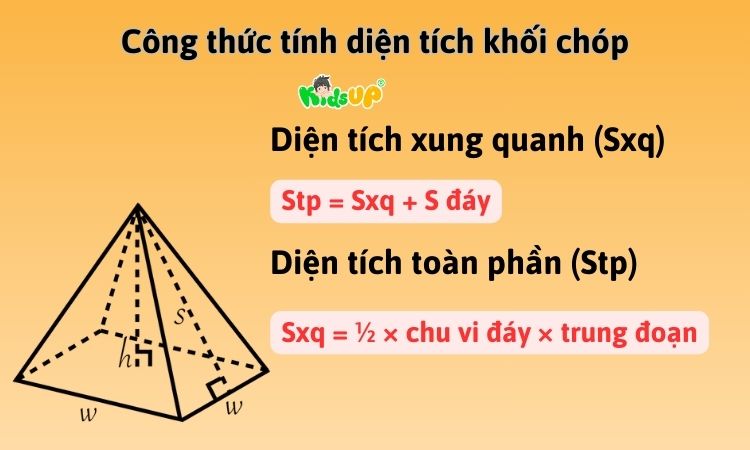
Diện tích xung quanh (Sxq)
Sxq = ½ × chu vi đáy × trung đoạn
Trong đó:
- Chu vi đáy là tổng độ dài các cạnh của đáy (tam giác, hình vuông, hình chữ nhật…).
- Trung đoạn là khoảng cách từ đỉnh chóp vuông góc xuống trung điểm cạnh đáy — cũng chính là chiều cao của các mặt bên nếu là khối chóp đều.
Diện tích toàn phần (Stp)
Stp = Sxq + S đáy
Tùy vào hình dạng mặt đáy mà cách tính S đáy sẽ khác nhau:
- Nếu đáy là tam giác, áp dụng công thức diện tích tam giác.
- Nếu là hình vuông hoặc chữ nhật, lấy tích chiều dài × chiều rộng.
- Với các hình đặc biệt khác, cần áp dụng công thức tương ứng theo hình học cơ bản.
Phương pháp học diện tích khối chóp không cần học thuộc lòng
Thay vì ép bản thân phải “học vẹt” các công thức khô khan, bạn hoàn toàn có thể tiếp cận diện tích khối chóp theo cách tự nhiên và dễ nhớ hơn. Phương pháp học thông minh tập trung vào việc hiểu bản chất, áp dụng thực tế và hệ thống hóa kiến thức một cách trực quan. Cùng khám phá từng cách học hiệu quả dưới đây!
Hiểu bản chất thay vì ghi nhớ
Thay vì ép bản thân phải học thuộc lòng công thức một cách máy móc, bạn nên bắt đầu từ việc hiểu cấu trúc và nguyên lý hình thành công thức. Mỗi công thức tính diện tích khối chóp đều dựa trên các yếu tố hình học quen thuộc như chu vi, trung đoạn, diện tích đáy. Hãy tưởng tượng khối chóp như một chiếc lều – trong đó đáy là mặt đất, các mặt bên là vải phủ xung quanh, còn trung đoạn là chiều cao của các mặt bên.
Việc sử dụng hình ảnh minh họa, mô hình giấy hoặc mô hình 3D không chỉ giúp học sinh dễ hình dung mà còn tạo ra kết nối trực quan giữa công thức và hình khối thực tế. Ngoài ra, hãy liên hệ công thức khối chóp với các kiến thức đã học như hình tam giác, hình vuông hay hình chữ nhật để hiểu sâu hơn cách tính toán.
Áp dụng công thức thông qua ví dụ thực tế
Một trong những cách học hiệu quả nhất là thực hành qua các ví dụ cụ thể. Hãy bắt đầu với bài toán đơn giản có số liệu rõ ràng, sau đó tăng dần độ khó. Khi giải, bạn nên phân tích từng bước: xác định loại đáy, tính chu vi hoặc diện tích đáy, xác định trung đoạn rồi thay vào công thức.
Không chỉ dừng lại ở việc tìm ra đáp án, bạn cần so sánh các bài toán đã giải, từ đó rút ra những điểm chung như hình dạng đáy nào thì công thức áp dụng ra sao, trung đoạn được tính từ đâu,… Những quy luật lặp lại sẽ giúp bạn không cần học thuộc lòng mà vẫn nhớ công thức một cách tự nhiên.
Vẽ sơ đồ tư duy hoặc bảng tóm tắt kiến thức
Hệ thống hóa kiến thức bằng sơ đồ tư duy sẽ giúp bạn nắm bắt được toàn bộ mối liên hệ giữa các loại khối chóp, cách tính diện tích xung quanh và toàn phần, cũng như mối liên kết giữa các đại lượng như chu vi đáy, trung đoạn, diện tích đáy. Bạn có thể vẽ một sơ đồ trung tâm là “Diện tích khối chóp”, phân nhánh ra thành “Sxq” và “Stp”, tiếp tục phân tích từng thành phần.

Bên cạnh đó, lập bảng tóm tắt so sánh giữa các loại đáy như tam giác, vuông, chữ nhật,… và công thức diện tích tương ứng sẽ giúp bạn dễ tra cứu khi cần ôn tập. Cách học này đặc biệt hiệu quả với những bạn học theo kiểu trực quan và thích tổng hợp thông tin ngắn gọn, dễ nhớ.
Bài tập thực hàng và đi kèm đáp án chi tiết
Bài tập 1: Tính diện tích xung quanh của khối chóp tam giác đều
Đề bài: Cho khối chóp tam giác đều S.ABC, có đáy là tam giác đều cạnh 6 cm. Trung đoạn (đường cao của mặt bên) là 5 cm. Tìm Sxq của khối chóp.
Hướng dẫn giải:
- Vì đáy là tam giác đều cạnh 6 cm → chu vi đáy P = 3 × 6 = 18 cm
- Trung đoạn (chiều cao mặt bên) đã cho là 5 cm
- Áp dụng công thức: Sxq = ½ × P × trung đoạn = ½ × 18 × 5 = 45 cm2
Đáp án: Sxq = 45 cm2
Bài tập 2: Tính diện tích toàn phần của khối chóp tứ giác đều
Đề bài: Cho khối chóp có đáy là hình vuông cạnh 4 cm. Chiều cao mặt bên (trung đoạn) là 6 cm. Tìm Stp của khối chóp.
Hướng dẫn giải:
- Đáy là hình vuông cạnh 4 cm → chu vi đáy P = 4 × 4 = 16 cm
- Trung đoạn = 6 cm
- Diện tích xung quanh: Sxq = ½ × 16 × 6 = 48 cm2
- Diện tích đáy: Sđáy = 4 × 4 = 16 cm2
- Diện tích toàn phần: Stp = Sxq + Sđáy = 48 + 16 = 64 cm2
Đáp án: Stp = 64 cm2
Kết Luận
Hy vọng qua bài viết này, bạn đã nắm được cách tính diện tích khối chóp một cách dễ hiểu và không cần học thuộc lòng. Với phương pháp học trực quan và bài tập thực hành cụ thể, việc ghi nhớ công thức sẽ trở nên nhẹ nhàng hơn bao giờ hết. Đừng quên đồng hành cùng KidsUP – ứng dụng học tập thông minh hỗ trợ trẻ phát triển tư duy toán học một cách tự nhiên và hiệu quả!