Trung điểm của đoạn thẳng là kiến thức hình học cơ bản nhưng lại đóng vai trò quan trọng trong nhiều dạng bài tập từ lớp 6 trở lên. Trong bài viết này, KidsUP sẽ hướng dẫn ba mẹ và các em học sinh cách tìm trung điểm đoạn thẳng một cách dễ hiểu, chính xác từng bước, kèm theo các mẹo học nhanh và hệ thống bài tập thực hành để ghi nhớ lâu hơn.
Hiểu đúng về trung điểm của đoạn thẳng
Khi ta có một đoạn thẳng có 2 điểm đầu và 1 điểm nằm giữa thì điểm nằm giữa đó được gọi là trung điểm. Ví dụ khi cho đoạn thẳng AB, thì trung điểm M là điểm sao cho AM = MB.
Trung điểm không chỉ xuất hiện trong các bài toán hình học phẳng mà còn có trong hệ tọa độ, giúp học sinh giải quyết các bài toán về khoảng cách, vector, tam giác, hình bình hành…

Ví dụ minh họa:
- Nếu đoạn thẳng AB có độ dài 10cm, thì trung điểm M chia đoạn AB thành hai đoạn AM và MB mỗi đoạn dài 5cm.
- Nếu A có tọa độ (x₁, y₁) và B có tọa độ (x₂, y₂) thì tọa độ trung điểm M được tính theo công thức:
M = (x₁ + x₂ / 2, y₁ + y₂ / 2 )
Việc hiểu khái niệm này là tiền đề quan trọng để học tốt hình học từ lớp 6 đến các lớp cao hơn.
Hướng dẫn từng bước tìm trung điểm đoạn thẳng
Để xác định trung điểm chính xác, bạn cần tuân theo ba bước cơ bản sau.
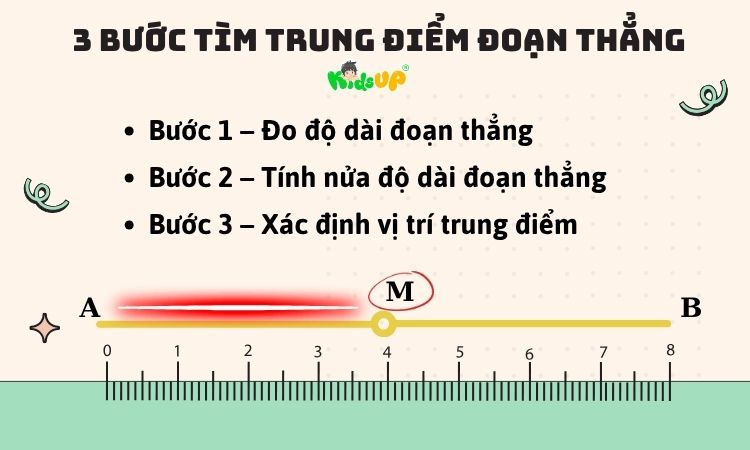
Bước 1 – Đo độ dài đoạn thẳng
Trước tiên, sử dụng thước để đo độ dài đoạn thẳng AB (nếu là bài tập hình vẽ). Đảm bảo đọc số chính xác đến đơn vị mm hoặc cm.
Ví dụ: Đo được AB = 8cm.
Trong trường hợp đoạn thẳng được cho trong hệ tọa độ, bạn cần áp dụng công thức tính khoảng cách hai điểm:
AB = √((x2 – x1)2 + (y2 – y1)2)
Bước 2 – Tính nửa độ dài đoạn thẳng
Chia đôi độ dài đoạn thẳng vừa đo được. Đây chính là khoảng cách từ điểm đầu hoặc điểm cuối đến trung điểm.
Ví dụ: AB = 8cm → AM = MB = 4cm.
Bước 3 – Đánh dấu trung điểm của đoạn thẳng
Dựa vào kết quả của bước 2, bạn đánh dấu điểm cách một đầu đoạn thẳng (ví dụ điểm A) một khoảng bằng nửa độ dài đã tính để xác định trung điểm M.
Nếu làm việc với tọa độ, bạn sử dụng công thức: M = (x₁ + x₂ / 2, y₁ + y₂ / 2 )
Đây là phương pháp nhanh, chính xác tuyệt đối khi làm bài kiểm tra trắc nghiệm hoặc đề thi.
Mẹo học nhanh và nhớ lâu trung điểm đoạn thẳng
Học lý thuyết thôi là chưa đủ, KidsUP gợi ý thêm một số mẹo nhỏ giúp các bé học nhanh và ghi nhớ kiến thức lâu hơn.

– Sử dụng hình ảnh minh họa
Trẻ em học nhanh hơn khi được tiếp xúc với hình ảnh sinh động. Ba mẹ có thể vẽ đoạn thẳng với trung điểm màu sắc nổi bật, dán lên góc học tập của bé hoặc dùng app học toán trực quan như KidsUP để bé tương tác trực tiếp.
– Áp dụng vào thực tế
Hãy khuyến khích trẻ xác định trung điểm trên các vật thể thực tế như cây thước, bàn học, sách vở… Điều này giúp trẻ hiểu rõ hơn về khái niệm “trung điểm” ngoài sách vở.
– Tạo trò chơi học tập
Dùng các trò chơi như “Tìm trung điểm nhanh nhất”, “Ai đoán đúng vị trí trung điểm” hoặc các trò chơi trong ứng dụng KidsUP giúp bé vừa học vừa chơi, tăng hiệu quả ghi nhớ.
Bài tập thực hành về trung điểm của đoạn thẳng
Để củng cố kiến thức, KidsUP gợi ý một số bài tập phù hợp với học sinh tiểu học và THCS:
– Bài tập 1 – Tìm trung điểm trên đoạn thẳng cho trước
Đề bài: Cho đoạn thẳng AB dài 12cm. Hãy xác định trung điểm M của đoạn AB.
Gợi ý giải:
- Đoạn AB = 12cm → AM = MB = 6cm.
- Trung điểm M nằm cách A hoặc B một khoảng 6cm.
Đề bài nâng cao: Cho đoạn thẳng CD dài 7,6cm. Đặt 1 dấu chấm để trung điểm E của đoạn thẳng CD.
– Bài tập 2 – Tìm trung điểm trong hệ tọa độ
Đề bài: Cho điểm A(2, 3) và điểm B(6, 7). Xác định tọa độ trung điểm M của đoạn thẳng nối AB.
Cách giải:
M = ((2 + 6) / 2, (3 + 7) / 2) = (4, 5)
Đề bài nâng cao: Cho C(–3, 2) và D(5, –6). Tính trung điểm của đoạn CD.
Ngoài ra, KidsUP cũng có các bài tập dạng trắc nghiệm tự luyện trên ứng dụng giúp bé rèn luyện kỹ năng giải toán mỗi ngày.
Kết luận
Trung điểm của đoạn thẳng là một khái niệm cơ bản nhưng vô cùng quan trọng trong Toán học. Việc nắm chắc cách tìm trung điểm không chỉ giúp các em giải nhanh các bài toán hình học mà còn xây dựng nền tảng tư duy logic vững chắc. Ba mẹ có thể đồng hành cùng con học toán dễ dàng hơn thông qua các ứng dụng giáo dục như KidsUP – nơi trẻ được học thông minh, thực hành tương tác và phát triển tư duy toàn diện.
Hãy đăng ký học thử KidsUP Soroban để trải nghiệm những giá trị mà app giáo dục này mang lại cho các con về mặt tư duy lâu dài.













