Con bạn đang học đến phần tam giác vuông mà vẫn chưa hiểu rõ khi nào hai tam giác được coi là bằng nhau? Đừng lo! Bài viết này của KidsUP sẽ giúp ba mẹ và các em học sinh nắm gọn các trường hợp bằng nhau của tam giác vuông theo đúng chương trình SGK. Nội dung dễ hiểu, ví dụ minh họa rõ ràng, giúp con học nhanh – nhớ lâu – làm bài tự tin!
Định nghĩa tam giác vuông theo SGK
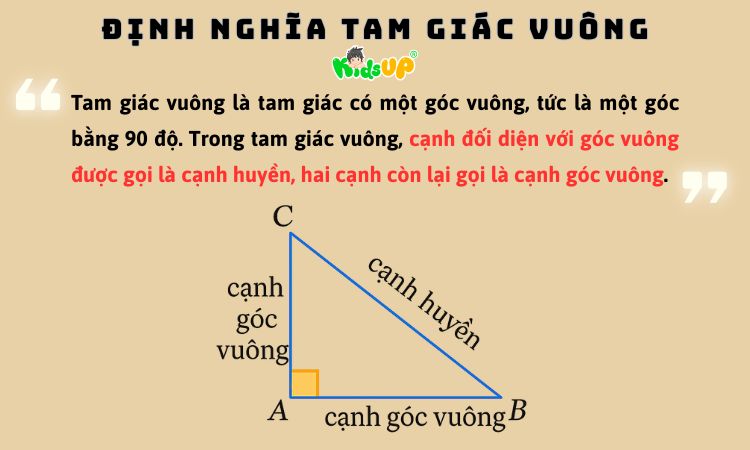
Theo chương trình SGK Toán lớp 7, tam giác vuông là tam giác có một góc vuông, tức là một góc bằng 90 độ. Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông.
Ví dụ: Tam giác ABC vuông tại A nghĩa là ∠A = 90°, khi đó cạnh BC là cạnh huyền, còn AB và AC là hai cạnh góc vuông.
Các trường hợp bằng nhau của tam giác vuông
Dưới đây là 3 trường hợp cơ bản và 1 trường hợp đặc biệt thường được sử dụng, bám sát nội dung trong SGK và có mở rộng để học sinh dễ tiếp cận:
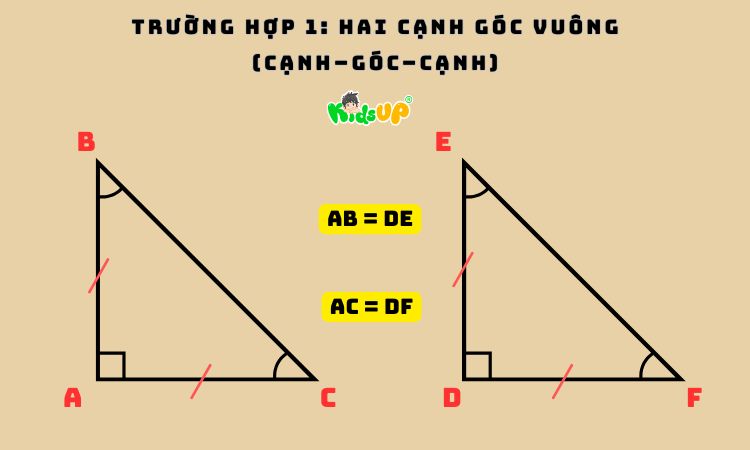
– Trường hợp 1: Hai cạnh góc vuông (cạnh–góc–cạnh)
Hai cạnh góc vuông của hai tam giác bằng nhau thì hai tam giác vuông đó sẽ bằng nhau.
Ví dụ thực tế: Tam giác vuông ABC và tam giác vuông DEF có AB = DE và AC = DF thì hai tam giác này đủ điều kiện để bằng nhau. Đây là trường hợp dễ nhận biết và dễ kiểm tra nhất trong bài tập hoặc thực hành đo đạc.
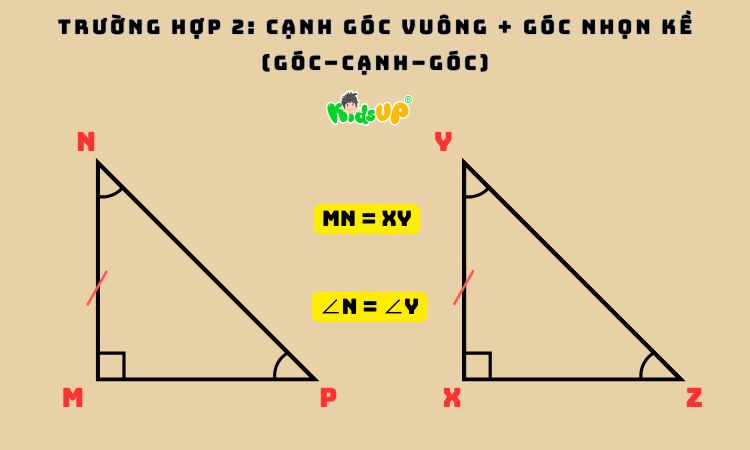
– Trường hợp 2: Cạnh góc vuông + góc nhọn kề (góc–cạnh–góc)
Hai tam giác vuông bằng nhau nếu có một cạnh góc vuông và một góc nhọn kề cạnh đó tương ứng bằng nhau.
Ví dụ thực tế: Tam giác vuông MNP và tam giác vuông XYZ có MN = XY và ∠N = ∠Y. Khi đó, hai tam giác này đã đảm bảo điều kiện để bằng nhau. Trường hợp này giúp học sinh vận dụng linh hoạt khi đề bài cho dữ kiện về góc và cạnh liền kề.
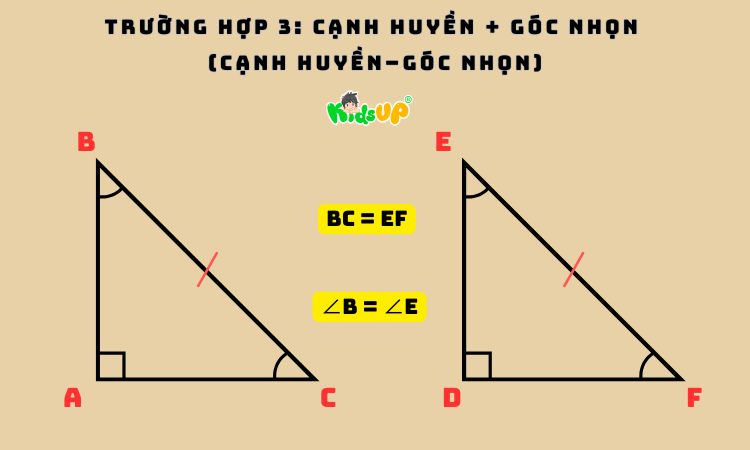
– Trường hợp 3: Cạnh huyền + góc nhọn (cạnh huyền–góc nhọn)
Cạnh huyền và một góc nhọn tương ứng bằng nhau là trường hợp thứ 3 tạo ra được 2 tam giác vuông bằng nhau. Ví dụ thực tế: Tam giác ABC và tam giác DEF đều vuông tại A và D, có BC = EF và ∠B = ∠E thì ABC = DEF.
Trường hợp này thường gặp trong các bài toán yêu cầu chứng minh tam giác bằng nhau khi biết số đo cạnh dài nhất và một góc.
– Trường hợp đặc biệt: Cạnh huyền và cạnh góc vuông
Mặc dù không được ghi rõ trong một số SGK, nhưng đây là trường hợp đặc biệt rất hữu ích và dễ hiểu, thường được nhiều giáo viên và học sinh sử dụng:
Cạnh huyền và một cạnh góc vuông của một tam giác vuông mà bằng nhau, thì hai tam giác vuông đó sẽ bằng nhau. Ví dụ: Tam giác ABC vuông tại A và tam giác DEF vuông tại D, nếu BC = EF (cạnh huyền) và AB = DE (một cạnh góc vuông), thì hai tam giác bằng nhau.
Vì sao nên học thêm trường hợp này?
– Dễ học, dễ nhớ: Không cần nhớ đến góc – chỉ cần 2 cạnh.
– Ứng dụng thực tiễn cao: Hay xuất hiện trong bài toán dựng hình, bài toán thực tế như đo đạc, thiết kế.
– Tránh nhầm lẫn: Học sinh dễ bị sai nếu chỉ nhớ “hai cạnh bằng nhau” mà không biết phân biệt cạnh nào. Việc thêm trường hợp này giúp tổng quát và hệ thống hóa kiến thức tốt hơn.
Bài tập vận dụng nâng cao – Có lời giải chi tiết
– Dạng 1: Chọn thêm điều kiện để chứng minh tam giác vuông bằng nhau
Bài 1: Cho tam giác vuông ABC vuông tại A và tam giác DEF vuông tại D. Biết AB = DE, ∠ABC = ∠DEF. Hỏi cần bổ sung điều kiện nào để chứng minh hai tam giác bằng nhau?
Lời giải:
– Ta đã có:
• Một cạnh góc vuông AB = DE
• Một góc nhọn ∠ABC = ∠DEF
– Đây gần giống trường hợp gcg, tuy nhiên cạnh AB không kề với góc ∠ABC ⇒ chưa đủ.
Cần bổ sung: cạnh AC = DF (cạnh góc vuông còn lại) → Áp dụng trường hợp cgv – cgv để kết luận:
ΔABC = ΔDEF (theo trường hợp hai cạnh góc vuông bằng nhau)
– Dạng 2: Tính độ dài hoặc góc bằng cách áp dụng trường hợp bằng nhau
Bài 2: Cho ΔABC vuông tại A, AB = 6cm, AC = 10cm. ΔMEF vuông tại M, có ME = 6cm, MF = 10cm. Tính độ dài cạnh BC và cạnh EF.
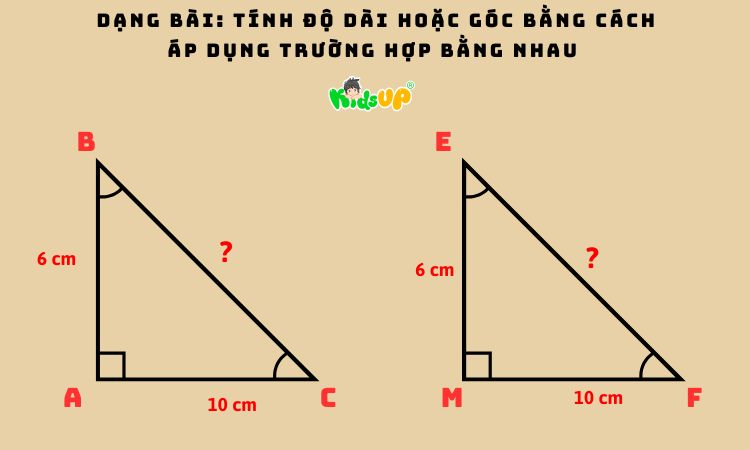
Lời giải:
– Ta có: AB = DE, AC = DF → Hai cạnh góc vuông tương ứng bằng nhau
⇒ ΔABC = ΔDEF (theo trường hợp cgv – cgv)
⇒ Hai cạnh tương ứng bằng nhau ⇒ BC = EF
Áp dụng định lý Pythagore cho ΔABC: BC² = AB² + AC² = 6² + 10² = 36 + 100 = 136 ⇒ BC = √136 = 11,66 cm
⇒ EF = 11,66 cm
– Dạng 3: Bài tập mở rộng – Ứng dụng trường hợp đặc biệt trong tam giác vuông cân
Bài 3: Cho tam giác BCD vuông tại B, BC = BD. Gọi D là điểm sao cho tam giác DEF vuông tại D, có DE = AB và DF = AC. Chứng minh ΔABC = ΔDEF.
Lời giải:
– Vì AB = AC ⇒ ΔABC là tam giác vuông cân tại A
– DE = AB, DF = AC ⇒ DE = DF ⇒ ΔDEF cũng là tam giác vuông cân tại D
→ Hai tam giác có:
• Cạnh huyền BC = EF (vì cùng được tính theo định lý Pythagore)
• Hai cạnh góc vuông có chiều dài bằng nhau.
⇒ ΔABC = ΔDEF (theo trường hợp đặc biệt: cạnh huyền và một cạnh góc vuông bằng nhau)
Câu hỏi thường gặp về trường hợp bằng nhau của tam giác vuông
– Câu hỏi 1: Có bao nhiêu trường hợp bằng nhau của tam giác vuông cần nhớ?
Theo chương trình SGK Toán THCS, học sinh cần ghi nhớ 3 trường hợp cơ bản sau:
- Hai cạnh góc vuông bằng nhau (cgv – cgv)
- Một cạnh góc vuông và góc nhọn kề bằng nhau (gcg)
- Cạnh huyền và một góc nhọn bằng nhau (chg)
Ngoài ra, có thể học thêm một trường hợp đặc biệt rất hữu ích trong thực tế:
- Cạnh huyền và một cạnh góc vuông bằng nhau (ch – cgv)
Đây là trường hợp mở rộng giúp học sinh dễ ghi nhớ, dễ áp dụng trong các bài toán dựng hình hoặc chứng minh ngắn gọn.
– Câu hỏi 2: Làm sao để tránh nhầm giữa cạnh huyền và cạnh góc vuông khi chứng minh?
Nhớ định nghĩa rõ ràng:
- Cạnh huyền: là cạnh dài nhất trong tam giác vuông, đối diện với góc vuông.
- Cạnh góc vuông: là hai cạnh có chung 1 điểm tạo thành góc vuông trong một hình tam giác vuông.
Quan sát ký hiệu góc vuông:
- Khi có ký hiệu hình vuông ở đỉnh (ví dụ ∠A vuông), cạnh đối diện (BC) chính là cạnh huyền.
- Cạnh nằm kề hai bên góc vuông (AB, AC) là hai cạnh góc vuông.
Mẹo ghi nhớ nhanh:
- “Huyền – hướng đối”: Cạnh huyền luôn nằm đối diện góc vuông.
- Trong hình vẽ tam giác vuông, nếu xác định được góc vuông rồi thì nhìn sang đối diện sẽ thấy ngay cạnh huyền!
Kết Luận
Hiểu rõ các trường hợp bằng nhau của tam giác vuông không chỉ giúp học sinh nắm vững kiến thức hình học mà còn tự tin hơn trong các bài kiểm tra và kỳ thi. Với ứng dụng học thông minh KidsUP, ba mẹ có thể đồng hành cùng con ôn tập hiệu quả, ghi nhớ kiến thức nhanh chóng và hứng thú hơn mỗi ngày.
