Hàm số bậc hai: Công thức, đồ thị và cách giải chi tiết

Trong chương trình toán học phổ thông, kiến thức về hàm số bậc hai là nền tảng vững chắc cho những khám phá sâu rộng hơn. Vậy ta có thể hiểu thế nào là một hàm số bậc hai? Làm thế nào để giải một bài toán liên quan tới dạng hàm này? Các bạn học sinh hãy cùng KidsUP tìm hiểu kĩ hơn trong bài viết dưới đây nhé!

Tổng quan về hàm số bậc hai

Hàm số bậc hai là một trong những khái niệm nền tảng của đại số. Do đó, nắm vững định nghĩa cơ bản và các tính chất của hàm số bậc hai không chỉ giúp bạn giải quyết các bài toán trong chương trình học mà còn xây dựng tư duy logic và khả năng phân tích vấn đề một cách hệ thống.

Định nghĩa và công thức tổng quát

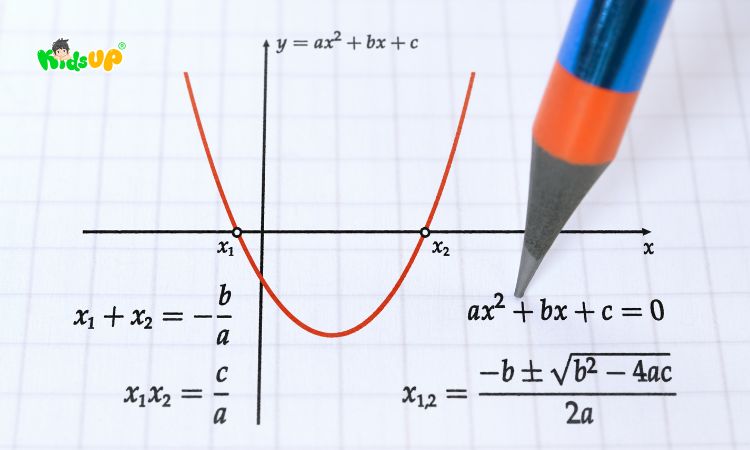
Hàm số bậc hai là hàm số có đồ thị là một parabol, được xác định bởi công thức tổng quát:

y = ax^2+bx+c

Trong đó 

• x là biến số và a, b, và c là các hằng số thực (a0). 
• Hệ số a quyết định hướng của parabol (đồ thị của hàm số)
• Hệ số b ảnh hưởng đến vị trí của đỉnh parabol
• Hệ số c là tung độ giao điểm của đồ thị với trục tung (trục Oy).

Ví dụ, các hàm số sau đều là hàm số bậc hai:

• y=2x2−3x+1 (với a=2, b=−3, c=1)
• y=−x2+5 (với a=−1, b=0, c=5)
• y=​x2+x−7 (với a=1​, b=1, c=−7)

Tính chất cơ bản

Đối với một hàm số bậc hai, nắm vững tính chất cơ bản trong đồ thị của hàm số sẽ giúp học sinh dễ dàng hình dung và hiểu rõ về kiến thức này. Một hàm số bậc hai sẽ có những đặc điểm, tính chất sau:

• Hàm số bậc hai có đồ thị luôn là một đường cong parabol, có một trục đối xứng đi qua đỉnh và song song với trục tung.
• Đồ thị parabol có thể hướng lên trên (khi a>0) hoặc hướng xuống dưới (khi a<0). 
• Đỉnh của parabol là giá trị lớn nhất (nếu a<0) hoặc giá trị nhỏ nhất (nếu a>0). 
• Hoành độ của đỉnh parabol được tính bằng công thức x=−b2a​, và tung độ tương ứng có thể tìm được bằng cách thay giá trị x này vào công thức của hàm số.

Đồ thị của hàm số bậc hai

Đồ thị của hàm số bậc hai là một đường cong parabol đối xứng, mang những đặc điểm hình học riêng biệt. Nắm vững hình dạng và các yếu tố xác định đồ thị parabol sẽ hữu ích trong quá trình học sinh phân tích và giải quyết các bài toán liên quan.

Hình dạng và đặc điểm của đồ thị

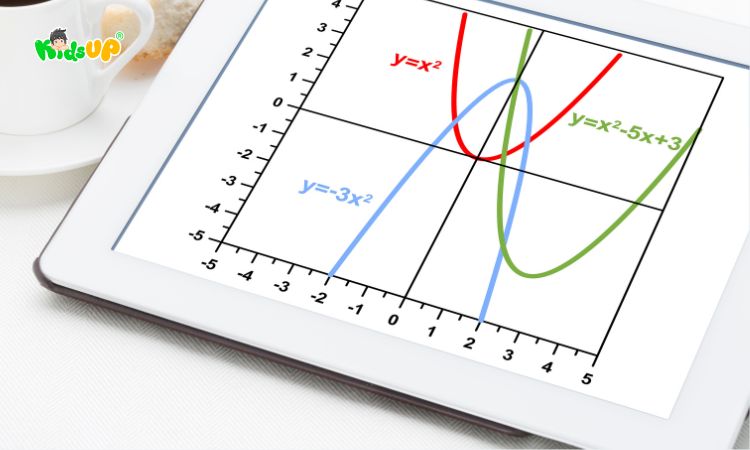
Như đã đề cập đến ở trên, đồ thị của hàm số bậc hai luôn là một đường parabol và hình dạng của parabol này phụ thuộc hoàn toàn vào dấu của hệ số a:

• Nếu a>0, đồ thị hàm bậc hai sẽ có bề lõm hướng lên trên. Điểm thấp nhất của parabol chính là đỉnh, và tại đó hàm số đạt giá trị nhỏ nhất.
• Nếu a<0, đồ thị hàm bậc hai sẽ có bề lõm hướng xuống dưới. Điểm cao nhất của parabol chính là đỉnh, và tại đó hàm số đạt giá trị lớn nhất.

Ngoài hệ số a, các hệ số b và c cũng ảnh hưởng đến vị trí của parabol trên mặt phẳng tọa độ. 

• Hệ số c chính là tung độ giao điểm của parabol với trục tung (điểm (0,c)). 
• Đỉnh của parabol có tọa độ là (−b2a,− Δ4a​), trong đó Δ=b2−4ac là biệt thức của phương trình bậc hai ax2+bx+c=0. 
• Trục đối xứng của parabol là đường thẳng thẳng đứng đi qua đỉnh, có phương trình là x=−b2a.

– Cách vẽ đồ thị từng bước

Để vẽ đồ thị của hàm số bậc hai một cách chính xác, chúng ta có thể thực hiện theo các bước sau, dựa vào các đặc điểm đồ thị đã nêu trên:

Bước 1: Xác định hệ số a, b, và c. Từ công thức hàm số, xác định giá trị của các hệ số này để biết được hướng bề lõm của parabol (a>0 hay a<0) và tung độ giao điểm với trục tung (c).

Bước 2: Tìm tọa độ đỉnh của parabol. Sử dụng công thức hoành độ đỉnh x1​=−b2a​. Sau đó, thay giá trị xI​ vào công thức hàm số để tìm tung độ đỉnh y1​=a(x1)2+b(x1)+c. Vậy tọa độ đỉnh là (x1​​,y1​​).

Bước 3: Xác định trục đối xứng của parabol. Trục đối xứng là đường thẳng đứng đi qua đỉnh, có phương trình là x=x1​​=−b2a​.

Bước 4: Tìm các điểm đặc biệt khác (nếu cần).

• Giao điểm với trục tung: Cho x=0, ta được y=c. Điểm giao là (0,c).
• Giao điểm với trục hoành (nếu có): Giải phương trình bậc hai ax2+bx+c=0. 
• Nếu phương trình có hai nghiệm phân biệt x1​ và x2​, thì đồ thị cắt trục hoành tại hai điểm (x1​,0) và (x2​,0). 
• Nếu có nghiệm kép x0​, thì đồ thị tiếp xúc với trục hoành tại điểm (x0,0). 
• Nếu phương trình vô nghiệm, đồ thị của hàm số bậc hai sẽ không cắt trục hoành.

Các điểm đối xứng: Chọn một vài giá trị x khác x1 và tính giá trị y tương ứng. Sau đó, sử dụng tính đối xứng của parabol qua trục x=x1​ để tìm các điểm đối xứng tương ứng. 

– Bước 5: Vẽ đồ thị. Học sinh dựa vào đỉnh, trục đối xứng và các điểm đặc biệt đã tìm được, vẽ đường cong parabol đi qua các điểm này một cách mềm mại và đối xứng.

Phương pháp giải phương trình bậc hai

Dưới đây là 3 phương pháp giải phương trình bậc 2 mà người học nên lưu lại để ứng dụng nhanh khi cần.

Phương pháp 1- Sử dụng công thức nghiệm

Đây là phương pháp tổng quát và luôn có thể áp dụng để giải mọi phương trình bậc hai có dạng ax2+bx+c=0 (a0). Phương pháp này đòi hỏi học sinh cần áp dụng biệt thức Δ=b2−4ac. Lợi ích của phương pháp này là tính tổng quát và dễ dàng áp dụng khi các hệ số a, b, c là các số cụ thể:

• Nếu Δ>0, phương trình có hai nghiệm thực phân biệt có công thức là: 

x1​=-b +Δ2a và x2​=-b –Δ2a

• Nếu Δ=0, phương trình có một nghiệm kép (hai nghiệm thực trùng nhau): 

x=−b2a

• Nếu Δ<0, phương trình không có nghiệm thực nào. Chúng ta thường kết luận là phương trình vô nghiệm thực.

Phương pháp 2 – Phân tích thành nhân tử

Phương pháp phân tích thành nhân tử áp dụng hiệu quả khi phương trình bậc hai có thể được biểu diễn dưới dạng tích của hai nhị thức bậc nhất. Tức là, chúng ta cố gắng viết ax2+bx+c=(mx+n)(px+q)=0. Khi đó, phương trình sẽ có nghiệm khi một trong hai nhân tử bằng không, tức là mx+n=0 hoặc px+q=0.

Ví dụ với phương trình x2−3x+2=0. 

• Chúng ta nhận thấy rằng x2−3x+2=(x−1)(x−2)=0. 
• Vậy, ta sẽ kết luận là phương trình có hai nghiệm tương ứng là x=1 và x=2.

Phương pháp 3 – Hoàn thành bình phương

Phương pháp hoàn thành bình phương là một kỹ thuật đại số để biến đổi phương trình bậc hai về dạng (x+h)2=k hoặc (x-h)2=k, từ đó dễ dàng tìm ra nghiệm bằng cách lấy căn bậc hai. 

Các bước cơ bản để giải phương trình ax2+bx+c=0 bằng phương pháp hoàn thành bình phương như sau:

1. Chia cả hai vế của phương trình cho a (nếu a1) để hệ số của x2 là 1: x2+ba​x+ca​=0.
2. Chuyển hằng số ca​sang vế phải: x2+ba​x=−ca​.
3. Thêm vào cả hai vế (b2a)2 để vế trái trở thành một bình phương hoàn chỉnh: x2+ba​x+(b2a)2=−ca​+(b2a)2
4. Viết vế trái dưới dạng bình phương của một tổng (hoặc hiệu): (x+b2a)2=b2-4ac4a2​=Δ4a2​.
5. Lấy căn bậc hai của cả hai vế để tìm x+​b2a, sau đó giải ra x.

Các dạng bài tập thường gặp

Dạng 1: Tìm giá trị lớn nhất, nhỏ nhất của hàm số

Dạng bài tập này yêu cầu người học xác định giá trị lớn nhất hoặc nhỏ nhất của hàm số bậc hai trên một khoảng xác định cho trước, giúp học sinh hiểu rõ hơn về sự biến thiên và giới hạn giá trị của hàm số.

Để giải dạng bài này, chúng ta thường sử dụng đỉnh của parabol. Đối với hàm số bậc hai y= ax2+bx+c:

• Nếu a>0, hàm số đạt giá trị nhỏ nhất tại đỉnh x=−b2a​, và giá trị nhỏ nhất là y=a(−b2a)2+b(−b2a​)+c=−Δ4a​. Vậy nên, ta sẽ kết luận là hàm số không có giá trị lớn nhất trên toàn bộ tập số thực.
• Nếu a<0, hàm số đạt giá trị lớn nhất tại đỉnh x=−b2a​, và giá trị lớn nhất là y=−Δ4a​. Hàm số không có giá trị nhỏ nhất trên toàn bộ tập số thực.

Dạng 2: Tìm điều kiện để phương trình có nghiệm

Dạng bài tập này liên quan đến việc xác định các giá trị của tham số sao cho phương trình bậc hai có nghiệm thỏa mãn một số điều kiện nhất định. Tác dụng của dạng bài này là giúp người học hiểu rõ mối quan hệ giữa các hệ số của phương trình và tính chất của nghiệm.

Để giải dạng bài này, chúng ta thường dựa vào biệt thức Δ=b2−4ac

• Phương trình có nghiệm thực khi và chỉ khi Δ≥0.
• Phương trình có hai nghiệm thực phân biệt khi và chỉ khi Δ>0.
• Phương trình có nghiệm kép khi và chỉ khi Δ=0.
• Phương trình vô nghiệm thực khi và chỉ khi Δ<0.

Ngoài ra, để xét dấu của nghiệm, chúng ta cũng có thể sử dụng định lý Vi-ét (x1​+x2=–ba​và x1​x2=ca​) kết hợp với các điều kiện về dấu của nghiệm..

Dạng 3: Ứng dụng trong bài toán thực tế

Hàm số bậc hai xuất hiện trong nhiều bài toán thực tế, từ vật lý, kỹ thuật, đến kinh tế. Ứng dụng các bài toán hàm số bậc hai trong thực tế sẽ giúp chúng ta thấy được tính ứng dụng rộng rãi của kiến thức toán học vào cuộc sống.

Để giải các bài toán ứng dụng, chúng ta cần:

• Đọc kỹ đề bài, xác định các đại lượng đã cho và đại lượng cần tìm.
• Xây dựng mô hình toán học, thường là một hàm số bậc hai mô tả mối quan hệ giữa các đại lượng.
• Sử dụng các kiến thức về hàm số bậc hai (tìm đỉnh, nghiệm, giá trị lớn nhất, nhỏ nhất) để giải quyết bài toán trong mô hình.
• Trả lời câu hỏi của bài toán bằng ngôn ngữ thực tế.

Mẹo học và ghi nhớ nhanh

Để học và ghi nhớ kiến thức về hàm số bậc hai một cách hiệu quả, đòi hỏi chúng ta không chỉ nắm vững lý thuyết mà còn có những mẹo nhỏ giúp củng cố kiến thức và áp dụng nhanh chóng.

Mẹo 1: Sử dụng bảng biến thiên

Bảng biến thiên là một công cụ vô cùng hữu ích để học sinh tóm tắt và hình dung sự biến đổi của hàm số bậc hai. Bằng cách lập bảng biến thiên, chúng ta có thể dễ dàng xác định khoảng đồng biến, nghịch biến, vị trí đỉnh và giá trị cực trị của hàm số.

Để lập bảng biến thiên cho hàm số bậc hai, chúng ta cần xác định:

• Hoành độ đỉnh: x1​​=−b2a​.
• Chiều biến thiên:

• • • Nếu a>0, hàm số nghịch biến trên khoảng (−∞,x1​) và đồng biến trên khoảng (x1,+∞). Giá trị nhỏ nhất của hàm số là yI​ tại x=x1​.
    • Nếu a<0, hàm số đồng biến trên khoảng (−∞,x1) và nghịch biến trên khoảng (x1,+∞). Giá trị lớn nhất của hàm số là y1​ tại x=x1.

• Giới hạn của hàm số khi x→±∞:

• • Nếu a>0, limx→±∞​y=+∞.
  • Nếu a<0, limx→±∞​y=−∞.

Mẹo 2: Nhận diện nhanh đồ thị qua hệ số

Các hệ số a, b, và c của hàm số bậc hai luôn mang những thông tin quan trọng về đồ thị của nó. Học sinh cần nắm vững cách nhận diện nhanh các đặc điểm của đồ thị thông qua hệ số để tiết kiệm thời gian trong quá trình giải bài toán và có cái nhìn trực quan hơn về hàm số.

• Hệ số a: Quyết định hướng bề lõm của parabol (a>0: lõm lên, a<0: lõm xuống). Độ lớn của ∣a∣ ảnh hưởng đến độ “mở” của parabol ( ∣a∣ càng lớn, parabol càng hẹp).
• Hệ số c: Là tung độ giao điểm của parabol với trục tung (điểm (0,c)).
• Dấu của biệt thức Δ=b2−4ac: Quyết định số lượng giao điểm của parabol với trục hoành (Δ>0: 2 giao điểm, Δ=0: 1 giao điểm (tiếp xúc), Δ<0: không có giao điểm).
• Hoành độ đỉnh −b2a​: Xác định vị trí của trục đối xứng và đỉnh parabol trên trục hoành.

Bài tập vận dụng kiến thức hàm số bậc 2 (Có đáp án)

Bài tập cơ bản

Giải các phương trình bậc hai đơn giản sau:

1. x2−5x+6=0
2. 2x2+7x+3=0
3. −x2+4x−4=0
4. 3x2−2x−1=0
5. x2+2x+5=0
6. 4x2−9=0
7. x2−3x=0
8. −2x2+8=0
9. 5x2=0
10. x2+x−1=0

Đáp án:

1. x=2 hoặc x=3
2. x=−3 hoặc x=−21​
3. x=2 (nghiệm kép)
4. x=1 hoặc x=−31​
5. Vô nghiệm thực
6. x=23​ hoặc x=−23​
7. x=0 hoặc x=3
8. x=2 hoặc x=−2
9. x=0 (nghiệm kép)
10. x=2−1+5​​ hoặc x=2−1−5​​

Bài tập nâng cao

Giải các bài toán liên quan đến ứng dụng thực tế sau:

1. Một quả bóng được ném thẳng đứng lên trên từ độ cao 2 mét với vận tốc ban đầu 10 m/s. Độ cao của quả bóng so với mặt đất tại thời điểm t (giây) được cho bởi công thức h(t)=−5t2+10t+2. Tìm thời điểm quả bóng đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu.
2. Một người nông dân có 100 mét hàng rào muốn rào một mảnh đất hình chữ nhật dọc theo một bờ sông (không cần rào phía bờ sông). Tìm kích thước của mảnh đất để diện tích rào được là lớn nhất.

Đáp án:

1. Thời điểm quả bóng đạt độ cao lớn nhất là t=−102x(-5)​=1 giây. Độ cao lớn nhất là h(1)=−5(1)+10(1)+2=7 mét.
2. Gọi chiều dài của mảnh đất vuông góc với bờ sông là x (mét). Khi đó, chiều dài song song với bờ sông là 100−2x (mét). Diện tích của mảnh đất là S(x)=x(100−2x)=−2x2+100x. Đây là một hàm số bậc hai với a=−2<0. Diện tích lớn nhất đạt được tại đỉnh của parabol, với x=−1002x(-2)​​=25 mét. Chiều dài song song với bờ sông là 100−2×25=50 mét. Vậy kích thước của mảnh đất để diện tích lớn nhất là 25 mét x 50 mét, và diện tích lớn nhất là 25×50=1250 mét vuông.

Kết luận

Hàm số bậc hai là một khái niệm toán học nền tảng với nhiều ứng dụng quan trọng trong cả lý thuyết và thực tiễn. Qua bài viết này của KidsUP , chúng ta đã cùng nhau khám phá công thức tổng quát, đặc điểm đồ thị, các phương pháp giải phương trình liên quan.