Bạn có biết rằng thế giới toán học quanh ta vận hành trơn tru nhờ những con số tưởng chừng đơn giản? Trong đó, số nguyên là nền tảng không thể thiếu — từ phép tính cơ bản đến những ứng dụng thực tế như thời gian, tiền bạc hay nhiệt độ. Bài viết này của KidsUP sẽ giúp bạn hiểu rõ số nguyên là gì, tại sao nó lại quan trọng đến mức ai cũng cần biết, dù là học sinh, phụ huynh đang dạy cho con tại nhà!
Định nghĩa số nguyên
Số nguyên là tập hợp các số không có phần thập phân, bao gồm số âm, số 0 và số dương. Hay nói cách khác, số nguyên là những số như: -3, -2, -1, 0, 1, 2, 3,… Đây là một khái niệm cơ bản trong toán học, thường được sử dụng để biểu thị các giá trị đầy đủ, không chia nhỏ.

Phân loại số nguyên
- Số nguyên dương: là các số lớn hơn 0 như 1, 2, 3,…
- Số nguyên âm: là các số nhỏ hơn 0 như -1, -2, -3,…
- Số 0: là số nguyên đặc biệt, không thuộc nhóm âm cũng không thuộc nhóm dương.
Số nguyên giúp chúng ta dễ dàng biểu diễn các khái niệm như tăng – giảm nhiệt độ, lãi – lỗ tài chính hay vị trí trên trục số.
Tính chất của số nguyên
Số nguyên không chỉ là tập hợp những con số đơn giản mà còn ẩn chứa nhiều tính chất toán học thú vị. Việc hiểu rõ các đặc điểm này sẽ giúp học sinh vận dụng linh hoạt trong các phép tính và giải toán hiệu quả hơn. Trong phần dưới đây, chúng ta sẽ cùng khám phá hai nhóm tính chất quan trọng nhất của số nguyên: tính chất đại số và tính chất thứ tự.
Tính chất đại số
Các số nguyên tuân theo nhiều tính chất đại số cơ bản giống như các số tự nhiên, giúp việc tính toán trở nên logic và nhất quán.
- Tính chất giao hoán: Với phép cộng và phép nhân, thứ tự các số không ảnh hưởng đến kết quả. Ví dụ: 3 + (-5) = -5 + 3 hoặc (-2) × 4 = 4 × (-2)
- Tính chất kết hợp: Khi cộng hoặc nhân ba số nguyên, ta có thể nhóm chúng lại theo nhiều cách mà vẫn cho kết quả như nhau. Ví dụ: (2 + 3) + (-1) = 2 + (3 + (-1))
- Tính chất phân phối: Phép nhân phân phối với phép cộng hoặc phép trừ. Ví dụ: 2 × (3 + (-4)) = 2 × 3 + 2 × (-4)
- Phép trừ và chia không có tính chất giao hoán hay kết hợp, nên khi thực hiện các phép tính này cần lưu ý thứ tự.
Tính chất thứ tự
Bên cạnh các quy tắc về phép tính, số nguyên còn có tính chất liên quan đến thứ tự và so sánh, giúp chúng ta xác định vị trí và mối quan hệ giữa các số.
- Số nguyên âm luôn nhỏ hơn số 0, và số 0 luôn nhỏ hơn bất kỳ số nguyên dương nào. Ví dụ: -3 < 0 < 5
- Trên trục số, nếu một số nằm bên trái số khác thì nó nhỏ hơn số đó. Ví dụ: -7 nằm bên trái -2 nên -7 < -2
- Khi cộng cùng một số vào hai số nguyên, quan hệ thứ tự giữa chúng không thay đổi. Ví dụ: Nếu -6 < -5 thì -6 + 3 < -5 + 3
Số nguyên trên trục số
– Cách vẽ trục số và đánh dấu các số nguyên
Để biểu diễn số nguyên, ta sử dụng một trục số nằm ngang, giống như một chiếc thước dài vô hạn ở cả hai đầu:
- Bước 1: Vẽ một đường thẳng nằm ngang và chọn một điểm làm gốc (thường ký hiệu là số 0).
- Bước 2: Kẻ các vạch cách đều nhau về hai phía.
- Phía bên phải của số 0: đánh các số nguyên dương (1, 2, 3,…).
- Phía bên trái của số 0: đánh các số nguyên âm (-1, -2, -3,…).
Mỗi vạch trên trục tương ứng với một số nguyên và được đánh dấu rõ ràng.
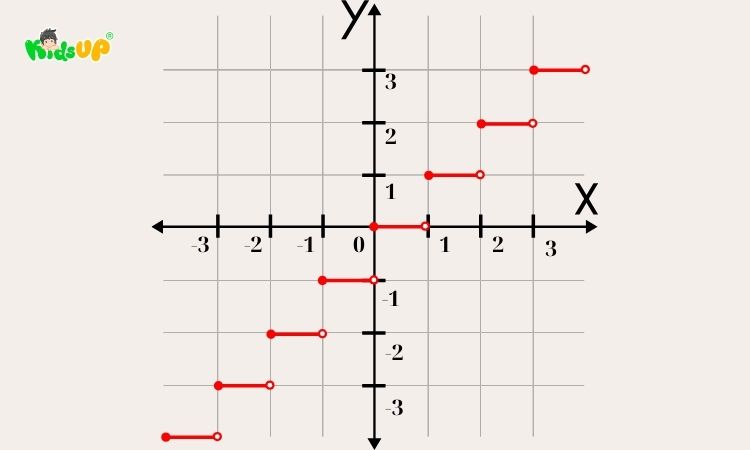
– Ý nghĩa của vị trí các số nguyên trên trục số
Vị trí của số nguyên trên trục số cho ta biết về giá trị và mối quan hệ giữa các số:
- Số càng nằm về bên phải thì càng lớn, số càng về bên trái thì càng nhỏ.
Ví dụ: -4 < -2 < 0 < 3 < 5 - Khoảng cách giữa các số nguyên là như nhau, thể hiện tính đều đặn của dãy số nguyên.
- Trục số giúp học sinh dễ hình dung khi làm các phép toán như cộng, trừ hoặc so sánh hai số nguyên.
Số nguyên trong thực tế
– Trong đời sống hàng ngày
Số nguyên xuất hiện rất nhiều trong các tình huống thực tế mà chúng ta gặp hàng ngày:
- Biểu thị nhiệt độ: Trong các bản tin thời tiết, nhiệt độ dưới 0°C được biểu thị bằng số nguyên âm, ví dụ: -5°C là trời rất lạnh, dưới mức đóng băng.
- Tính toán lãi/lỗ trong kinh doanh: Khi doanh thu cao hơn chi phí, kết quả là số dương (lãi); ngược lại, nếu chi phí vượt doanh thu, ta có số âm (lỗ).
- Xác định độ cao so với mực nước biển: Những vị trí dưới mực nước biển được ghi bằng số nguyên âm, ví dụ: -10m là thấp hơn mặt nước biển 10 mét.

Những ví dụ này cho thấy số nguyên không chỉ nằm trong sách vở mà còn phản ánh chân thực các hiện tượng trong đời sống.
– Trong các môn học khác
Ngoài toán học, số nguyên còn được ứng dụng rộng rãi trong nhiều môn học khác:
- Vật lý: Số nguyên được dùng để biểu diễn điện tích (âm và dương), chuyển động theo hai chiều ngược nhau, hoặc thay đổi nhiệt độ.
- Kinh tế: Trong bảng cân đối thu chi, số nguyên thể hiện lợi nhuận (dương) hoặc thua lỗ (âm).
- Tin học: Các chương trình máy tính thường sử dụng kiểu dữ liệu số nguyên để xử lý nhanh các phép toán, đếm vòng lặp, phân loại dữ liệu,…
Nhờ có số nguyên, việc tính toán, phân tích và mô hình hóa trong các môn học trở nên rõ ràng và chính xác hơn.
Mẹo học số nguyên hiệu quả
Hiểu và ghi nhớ kiến thức về số nguyên sẽ dễ dàng hơn nếu áp dụng đúng phương pháp. Dưới đây là một số mẹo giúp việc học số nguyên trở nên thú vị và hiệu quả hơn:
- Sử dụng trục số để hình dung và so sánh: Khi học số nguyên, hãy vẽ trục số và đánh dấu các con số để quan sát trực quan. Việc thấy được số nào nằm bên trái hay bên phải sẽ giúp học sinh hiểu rõ khái niệm lớn – bé và khoảng cách giữa các số.
- Thực hành phép toán thông qua bài tập: Càng luyện tập nhiều, học sinh càng dễ ghi nhớ các quy tắc cộng, trừ, nhân, chia với số nguyên. Nên bắt đầu từ bài đơn giản, sau đó tăng dần độ khó để tránh nhàm chán và tạo hứng thú học tập.
- Áp dụng vào các tình huống thực tế: Hãy kết nối bài học với cuộc sống như tính lãi/lỗ khi bán hàng, đo nhiệt độ, hay ghi lại độ cao khi leo núi. Việc này giúp học sinh thấy số nguyên không chỉ là lý thuyết mà còn rất hữu dụng trong đời sống hàng ngày.
Bài tập thực hành số nguyên (Có đáp án)
– Bài tập cơ bản về cộng, trừ, nhân, chia số nguyên
Câu 1: Tính:
a) 5 + (–3) = ?
b) –8 + (–2) = ?
c) –6 – (–4) = ?
d) (–3) × 4 = ?
e) (–12) ÷ (–3) = ?
Đáp án
a) 2
b) –10
c) –2
d) –12
e) 4
– Bài tập ứng dụng số nguyên trong các tình huống thực tế
Câu 2: Nhiệt độ buổi sáng là –2°C, buổi chiều tăng lên 5 độ. Hãy làm phép tính để tìm ra nhiệt độ của buổi chiều sau sau tăng độ?
→ Đáp án: –2 + 5 = 3°C
Câu 3: Một người bán hàng lỗ 15.000 đồng vào buổi sáng (ghi là –15.000), và lãi 20.000 đồng vào buổi chiều. Tính tổng lời/lỗ trong ngày đó.
→ Đáp án: –15.000 + 20.000 = 5.000 đồng (lãi)
Câu 4: Một người leo núi đang ở độ cao –50m (dưới mực nước biển). Nếu người đó leo lên thêm 80m thì sẽ ở độ cao bao nhiêu?
→ Đáp án: –50 + 80 = 30m
Kết Luận
Hy vọng qua bài viết này, ba mẹ và các em học sinh đã hiểu rõ hơn số nguyên là gì, cũng như cách áp dụng và học hiệu quả khái niệm quan trọng này. Để việc học trở nên thú vị và dễ tiếp thu hơn, ba mẹ có thể tham khảo ứng dụng KidsUP – trợ thủ học tập thông minh giúp trẻ rèn luyện toán học từ cơ bản đến nâng cao, bao gồm cả chủ đề số nguyên.