Bạn từng thắc mắc vì sao căn bậc hai lại xuất hiện khắp nơi trong toán học? Đừng lo! Bài viết này của KidsUP sẽ giúp bạn hiểu rõ căn bậc hai số học là gì, cách tính nhanh, dễ nhớ và tránh nhầm lẫn với căn bậc hai đại số. Phụ huynh, học sinh hay giáo viên đều có thể áp dụng ngay để học tốt hơn và giảng dạy hiệu quả hơn!
Định nghĩa căn bậc hai số học
Căn bậc hai số học của một số không âm là một số không âm mà bình phương của nó bằng chính số đó. Nói đơn giản hơn, nếu x là căn bậc hai của a, thì x² = a và x ≥ 0.
Ví dụ:
- √9 = 3 vì 3² = 9
- √0 = 0
Căn bậc hai số học chỉ áp dụng cho số không âm và luôn cho kết quả không âm.
Phân biệt với căn bậc hai đại số
Nhiều học sinh dễ nhầm lẫn giữa căn bậc hai số học và căn bậc hai đại số.
- Căn bậc hai số học: chỉ lấy giá trị không âm, ví dụ: √16 = 4
- Căn bậc hai đại số: bao gồm cả giá trị âm và dương: x² = 16 ⇒ x = ±4
⇒ Khi không nói rõ, mặc định hiểu là căn bậc hai số học.
Các phương pháp tính căn bậc hai số học
– Nhẩm kết quả dựa trên bình phương
Áp dụng cho các số chính phương quen thuộc:
- √1 = 1
- √4 = 2
- √9 = 3
– Phép chia và lặp (Babylonian method)
Áp dụng cho số không phải chính phương:
Giả sử số cần tìm căn là S:
- Chọn giá trị gần đúng ban đầu: x₀
- Áp dụng công thức: xₙ₊₁ = ½(xₙ + S / xₙ)
– Dùng máy tính: Sử dụng máy tính hoặc các ứng dụng học tập như KidsUP để tính nhanh và chính xác.
Tính chất chuẩn về căn bậc hai số học
Căn bậc hai số học có nhiều tính chất quan trọng giúp học sinh rút gọn biểu thức và giải toán nhanh hơn. Dưới đây là các tính chất phổ biến và cách giải thích đơn giản để học sinh dễ hiểu và áp dụng.
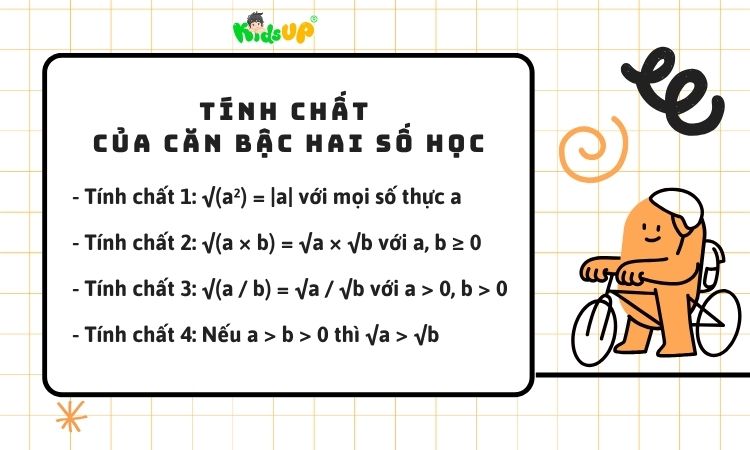
– Tính chất 1: √(a²) = |a| với mọi số thực a
Giải thích: Khi bình phương một số bất kỳ (kể cả âm), kết quả luôn là số dương. Nhưng khi lấy căn bậc hai, ta chỉ lấy giá trị không âm, nên kết quả là giá trị tuyệt đối của a.
Ví dụ:
- √(5²) = √25 = 5
- √((-5)²) = √25 = 5 (không phải -5)
- √(0²) = √0 = 0
– Tính chất 2: √(a × b) = √a × √b với a, b ≥ 0
Giải thích: Nếu cả hai số đều không âm, bạn có thể tách dấu căn thành tích của hai căn riêng biệt. Đây là cách rút gọn thường dùng trong bài tập đại số.
Ví dụ:
- √(4 × 9) = √36 = 6
- √4 × √9 = 2 × 3 = 6
⇒ Hai cách đều cho ra kết quả như nhau.
– Tính chất 3: √(a / b) = √a / √b với a > 0, b > 0
Giải thích: Khi chia hai số dương, căn bậc hai của thương bằng thương của hai căn bậc hai.
Ví dụ:
- √(49 / 4) = √49 / √4 = 7 / 2
- √(9 / 25) = √9 / √25 = 3 / 5
Lưu ý: Không áp dụng nếu mẫu số bằng 0.
– Tính chất 4: Nếu a > b > 0 thì √a > √b
Giải thích: Hàm căn bậc hai là hàm đồng biến, nghĩa là số lớn hơn sẽ có căn lớn hơn. Đây là cơ sở cho các bài toán so sánh giá trị căn bậc hai.
Ví dụ:
- √16 = 4 và √9 = 3 ⇒ 4 > 3
- Vì 16 > 9 nên √16 > √9
Ứng dụng của căn bậc hai số học trong thực tế
Kiến thức này không chỉ là một khái niệm trừu tượng trong sách vở mà còn có thể được áp dụng trong cuộc sống và trong những công việc yêu cầu. Dưới đây là hai lĩnh vực mà căn bậc hai thường xuyên xuất hiện và được sử dụng:
– Trong hình học: Trong chương trình toán học cấp 2, đặc biệt là hình học, căn bậc hai thường xuất hiện khi áp dụng định lý Pythagoras.
– Tính độ dài cạnh trong tam giác vuông:
- Nếu biết hai cạnh góc vuông, có thể tính cạnh huyền bằng công thức: √(a² + b²)
- Ví dụ: Một tam giác vuông có hai cạnh góc vuông là 3 cm và 4 cm. Khi đó cạnh huyền là: √(3² + 4²) = √(9 + 16) = √25 = 5 cm
– Tính đường chéo hình vuông, hình chữ nhật:
- Đường chéo hình vuông cạnh a: √(a² + a²) = a√2
- Đường chéo hình chữ nhật: √(chiều dài² + chiều rộng²)
- Tính diện tích: Trong một số trường hợp, muốn tính cạnh của hình vuông khi biết diện tích, ta phải lấy căn bậc hai của diện tích.
Ví dụ: Diện tích hình vuông là 121 cm² ⇒ cạnh là √121 = 11 cm
Căn bậc hai giúp học sinh hiểu sâu hơn về mối quan hệ giữa các cạnh trong hình học và phát triển tư duy logic, không đơn thuần chỉ là kỹ thuật tính toán.
– Trong vật lý
Căn bậc hai cũng xuất hiện thường xuyên trong các công thức vật lý cơ bản, nhất là trong những bài học liên quan đến chuyển động, vận tốc, năng lượng,…
- Tính tốc độ trung bình: Khi biết quãng đường và thời gian, đôi khi người học phải tìm tốc độ bằng cách rút gọn công thức chứa căn.
- Tính gia tốc hoặc vận tốc: Một số bài toán yêu cầu áp dụng công thức: v = √(2as)
Với:
- v là vận tốc cuối
- a là gia tốc
- s là quãng đường
Mẹo học nhanh căn bậc hai số học
- Học thuộc bảng bình phương từ 1² đến 20²
- Ghi nhớ bảng căn bậc hai thông dụng
- Học qua trò chơi tương tác hoặc ứng dụng như KidsUP
- Liên hệ thực tế: cạnh hình vuông, toán đo lường, v.v.
Bài tập luyện tập căn bậc hai số học
– Bài tập cơ bản
- Tính: √49, √100, √0, √81
- Đúng hay sai:
- √25 = -5
- √1 = 1
- Viết các số chính phương từ 1 đến 100
– Bài tập nâng cao
- Rút gọn:
- √36 × 25
- √144 / 16
- Tính gần đúng:
- √2 ≈ ?
- √10 ≈ ?
- Bài toán thực tế: Một hình vuông có diện tích 121 cm². Tính cạnh hình vuông đó.
Kết luận
Căn bậc hai số học là khái niệm nền tảng trong chương trình toán học từ lớp 6 trở lên. Việc hiểu rõ cách tính, tính chất và ứng dụng của nó giúp học sinh phát triển tư duy toán học logic và vững vàng hơn khi làm bài. Nếu bạn là phụ huynh hoặc giáo viên muốn đồng hành cùng trẻ trong quá trình học tập, hãy để KidsUP trở thành người bạn đồng hành qua những bài học thú vị và dễ hiểu!
