

Hôm nay, chúng ta sẽ cùng khám phá một hình học vô cùng quen thuộc hình tam giác nhé! Hình tam giác có ba cạnh và ba góc, và ẩn chứa rất nhiều điều thú vị. Khi học về hình tam giác, các bạn sẽ nắm được các tính chất cơ bản, công thức tính chu vi và diện tích nữa. Trong bài viết này, KidsUP sẽ giúp bạn hiểu rõ hơn về hình tam giác, để các bạn tự tin giải các bài toán và áp dụng vào thực tế
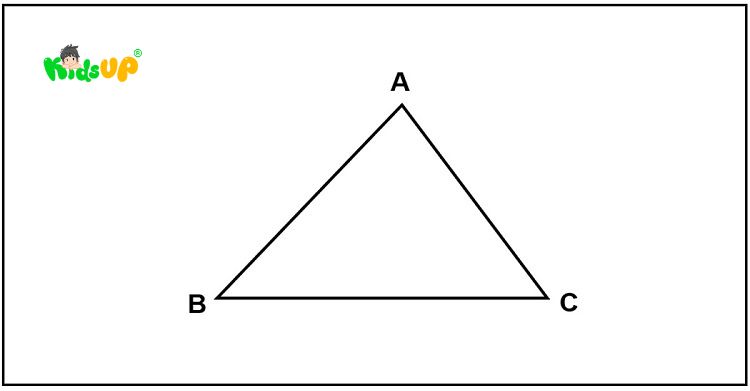
Hình tam giác được tạo thành từ ba đoạn thẳng nối ba điểm không thẳng hàng. Những điểm này gọi là ba đỉnh của tam giác. Các đoạn thẳng nối chúng là ba cạnh của tam giác. Tam giác cũng có ba góc tạo thành từ ba cặp cạnh, và tổng ba góc trong của bất kỳ tam giác nào luôn bằng 180 độ.
Phân loại hình tam giác theo độ dài cạnh:
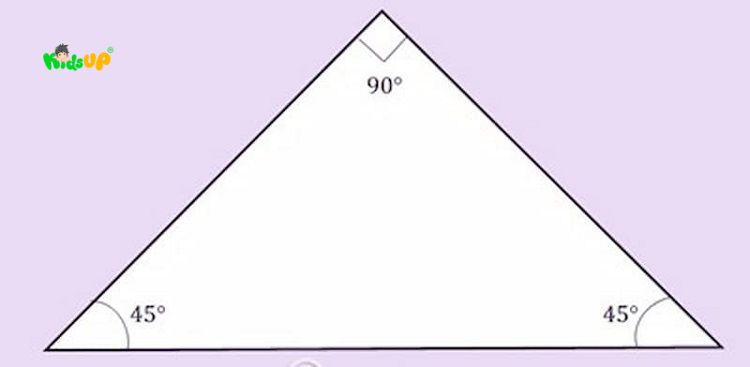
Phân loại hình tam giác theo độ của góc:
Hình tam giác là đa giác đơn giản nhất, gồm ba cạnh và ba góc. Dưới đây là những tính chất cơ bản, giúp các em nắm chắc kiến thức và áp dụng giải toán hiệu quả:
∠A + ∠B + ∠C = 180°
a + b > c, b + c > a, c + a > b
Nếu a > b thì ∠A > ∠B
Góc ngoài tại A = ∠B + ∠C
S = ½ × đáy × đường cao
6. Đường trung trực (vuông góc tại trung điểm cạnh) là tập hợp các điểm cách đều hai đầu mút cạnh đó.

Tổng độ dài của hai cạnh bất kỳ trong một tam giác sẽ luôn lớn hơn độ dài của cạnh còn lại. Tính chất này còn được gọi là bất đẳng thức tam giác. Đây là một nguyên tắc quan trọng khi xác định độ dài các cạnh trong tam giác.
Chu vi của một tam giác được xác định bằng tổng độ dài ba cạnh của tam giác đó. Công thức tính chu vi hình tam giác áp dụng cho mọi loại tam giác, dù là tam giác đều, tam giác cân, tam giác vuông, hay tam giác thường.
Giả sử một tam giác có ba cạnh là b, a và c. Khi đó, chu vi của tam giác được tính theo công thức: P = a + b + c
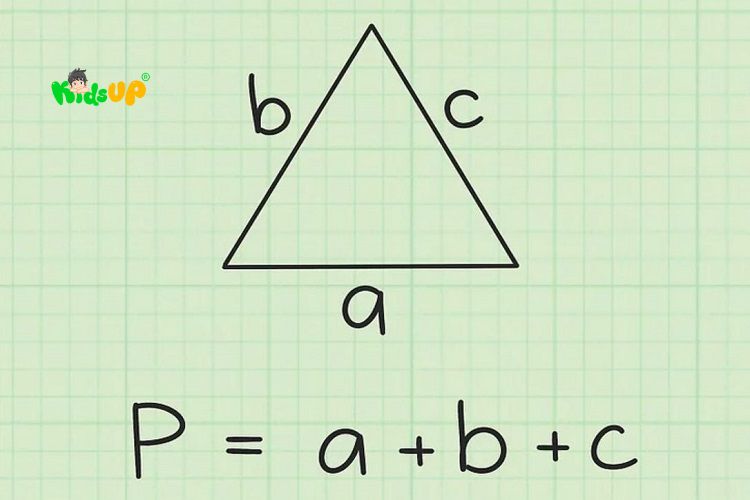
Bài tập thực hành chu vi hình tam giác:
Bài 1: Tam giác ABC có ba cạnh a = 6cm, b = 7cm, c = 9 cm. Hãy tính chu vi tam giác.
Bài 2: Một tam giác đều có cạnh dài 9 cm. Tính chu vi của tam giác này.
Bài 3: Một tam giác vuông có cạnh góc vuông thứ nhất dài 6 cm, cạnh góc vuông thứ hai dài 8 cm, và cạnh huyền dài 10 cm. Tính chu vi của tam giác này.
Lời giải:
Bài 1: Chu vi tam giác là: 6 + 7 + 9 = 22 (cm)
Bài 2: Chu vi tam giác là: 9 x 3 = 27 (cm)
Bài 3: Chu vi tam giác là: 6 + 8 + 10 = 24 (cm)
Diện tích của một tam giác là phần không gian được bao quanh bởi ba cạnh của tam giác đó. Có nhiều cách tính diện tích tùy vào loại tam giác và thông tin cho trước.
Đối với một hình tam giác bất kỳ, công thức tính diện tích sẽ là: S = ½ × đáy × chiều cao
Trong đó:
– Trường hợp đặc biệt:
– Bài tập thực hành tính diện tích hình tam giác
Bài 1: Tam giác ABC có cạnh đáy a=10 cm, chiều cao h=5 cm. Tính diện tích tam giác ABC.
Bài 2: Tam giác vuông BCD có hai cạnh góc vuông là 10 và 8. Tính diện tích tam giác BCD.
Lời giải:
Bài 1: Diện tích tam giác là: S = 1/2 x 10 x 5 = 25 cm2
Bài 2: Diện tích tam giác BCD: S = 1/2 x 10 x 8 = 40 cm2
Bài viết trên đã chia sẻ với bạn những công thức quan trọng khi tính hình tam giác. Đây là một trong những hình học cơ bản mà các bé cần nắm vững để làm các bài toán nâng cao về sau. Để trẻ được giáo dục sớm về toán tư duy ngay từ khi học mầm non thì KidsUP Pro với một hệ sinh thái tất cả trong một sẽ là một lựa chọn chất lượng đối với mọi trẻ từ 1 – 8 tuổi. Đăng ký học thử KidsUP Pro từ sớm để nhận được những ưu đãi tuyệt vời nhất từ ứng dụng giáo dục sớm ba mẹ nhé.

Chào các độc giả của KidsUP, mình là Khả Như – tác giả tại chuyên mục “Kiến thức giáo dục sớm”. Mình đã có 3 năm kinh nghiệm trong lĩnh vực biên soạn nội dung và chia sẻ kiến thức, kinh nghiệm trong các lĩnh vực giáo dục trẻ nhỏ, nuôi dạy con,…. Mình hy vọng rằng với những nội dung tâm huyết mình đăng tải trên sẽ đem tới cho các bậc phụ huynh cũng như các bé nhiều giá trị hữu ích.