Bạn đang loay hoay tìm cách giúp con mình hiểu nhanh và làm chủ phép nhân hai phân số? Đừng lo! Chỉ với một vài mẹo nhỏ đơn giản mà hiệu quả, bài viết này của KidsUP sẽ giúp học sinh tiểu học tiếp cách nhân hai phân số một cách dễ nhớ – dễ làm – dễ áp dụng vào bài tập.
Các bước nhân hai phân số đơn giản
Quá trình học cách nhân hai phân số không hề khó nếu học sinh hiểu rõ các bước thực hiện. Với mỗi phép nhân, các bạn học sinh chỉ cần ghi nhớ 3 bước cơ bản sau.

Bước 1: Nhân tử số với tử số
Để bạn đọc dễ dàng hình dung cách nhân hai phân số theo từng bước, KidsUP có một bài toán mẫu sau:
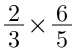
Ở bước 1, ta sẽ nhân tử số của hai phân số với nhau:
2 (tử số của phân số thứ nhất) × 4 (tử số của phân số thứ hai) = 8
=> Kết quả tử số mới của phân số tích là 8.
Bước 2: Nhân mẫu số với mẫu số
Sau khi đã tính được tử số của phép nhân, bước tiếp theo là nhân mẫu số với mẫu số. Mẫu số là phần nằm dưới dấu gạch ngang – thể hiện số phần bằng nhau mà một đơn vị được chia ra.
Chúng ta sẽ tiếp tục thực hiện bước 2 với ví dụ trên:
Ta đã có tử số là 8. Bây giờ, ta lấy mẫu số của hai phân số và nhân với nhau:
3 (mẫu của phân số thứ nhất) × 5 (mẫu của phân số thứ hai) = 15
Vậy kết quả sau khi thực hiện cả hai bước đầu là: 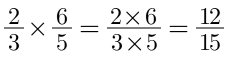
Bước 3: rút gọn nếu phân số chưa đủ tối giản (nếu đề bài yêu cầu)
Rút gọn phân số có nghĩa là chúng ta sẽ chia cả tử số và mẫu số của phân số cho cùng một số tự nhiên lớn hơn 1, sao cho không còn số tự nhiên nào lớn hơn 1 có thể chia hết cả hai số đó nữa. Phân số sau khi rút gọn được gọi là phân số tối giản.
Chúng ta sẽ tiếp tục với đáp án của phép nhân ở ví dụ trên
Các bạn có thể nhận thấy số 12 và số 15 đều có ước chung là 3, do đó ta sẽ thực hiện bước rút gọn phân số như sau:
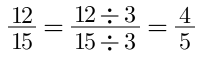
Mẹo làm phép nhân phân số dễ dàng
Sau khi đã nắm được cách nhân hai phân số, học sinh có thể áp dụng một vài mẹo nhỏ để quá trình tính toán trở nên đơn giản và dễ dàng hơn. Áp dụng linh hoạt các mẹo sẽ giúp học sinh tính toán gọn gàng hơn và hình thành tư duy Toán học linh hoạt.

– Rút gọn trước khi nhân
Một mẹo rất hiệu quả trong cách nhân hai phân số là rút gọn phân số trước khi thực hiện phép nhân. Mẹo này giúp đơn giản hóa các con số trong phép tính, làm cho việc nhân trở nên dễ dàng hơn và kết quả thu được thường đã ở dạng tối giản hoặc dễ rút gọn hơn rất nhiều. Thay vì chờ đến khi nhân xong mới rút gọn, ta có thể nhìn các cặp số tử và mẫu chéo để tìm cơ hội chia nhỏ trước.
Chẳng hạn như với phép nhân dưới đây:
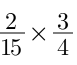
Ta nhận thấy các cặp tử và mẫu chéo (2, 4 và 3, 15) đều có thể rút gọn bằng cách chia cho ƯCLN của chúng, vậy nên ta sẽ có cách giải như sau:
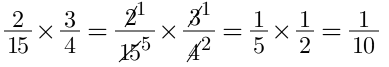
– Ứng dụng tính chất giao hoán và kết hợp
Trong phép nhân các số tự nhiên, chúng ta đã biết đến tính chất giao hoán (thứ tự các số nhân không ảnh hưởng đến kết quả) và tính chất kết hợp (có thể nhóm các số hạng lại để nhân theo thứ tự thuận tiện). Những tính chất này cũng hoàn toàn đúng với phép nhân phân số.
Chẳng hạn như với phép nhân mẫu dưới đây:
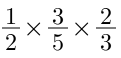
Nếu ta sử dụng tính chất kết hợp, ta sẽ dễ dàng rút gọn được phép nhân bằng cách rút gọn 2 phân số thứ 2 và thứ 3 như sau:

Tiếp tục tiến hành phép nhân, ta sẽ có đáp án là:
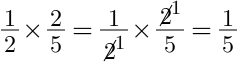
Các dạng bài tập cách nhân hai phân số thường gặp
Để thực sự làm chủ cách nhân hai phân số, thực hành qua các dạng bài tập khác nhau là vô cùng quan trọng. Khi học sinh được luyện tập thường xuyên, quá trình tiếp thu kiến thức sẽ trở nên đơn giản và dễ dàng hơn rất nhiều. Dưới đây là các dạng bài thường gặp về nhân hai phân số

Dạng 1 – Phép nhân hai phân số cơ bản
Đây là dạng bài cơ bản nhất, giúp học sinh làm quen với từng bước để nhân hai phân số: nhân tử với tử, mẫu với mẫu và rút gọn kết quả. Sau đây là một phép toán ví dụ mà bạn đọc có thể tham khảo
Ví dụ: Tính tích của phép nhân sau: 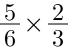
Áp dụng từng bước trong cách nhân hai phân số, ta sẽ đáp án là:
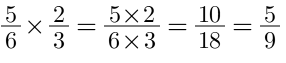
Dạng 2 – Tính giá trị biểu thức có nhiều phân số
Dạng bài này là phân nâng cao hơn của dạng bài tính tích cơ bản. Bài toán tính giá trị biểu thức có nhiều phân số yêu cầu học sinh cần phải linh hoạt để thực hiện phép nhân với nhiều phân số liên tiếp. Những bài toán này sẽ giúp học sinh rèn luyện khả năng rút gọn trước khi thực hiện phép nhân và áp dụng các tính chất để hoàn thành phép tính
Ví dụ: Tính giá trị của biểu thức phân số sau:
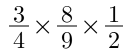
Đầu tiên, ta sẽ thực hiện bước rút gọn các cặp tử và mẫu có ƯCLN lớn hơn 1 là 8, 4 và 3, 9, ta sẽ có:
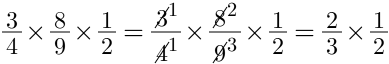
Tiếp tục thực hiện phép nhân, ta sẽ có đáp án là:
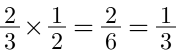
Dạng 3 – Bài toán có lời văn
Ví dụ: Một khu vườn hình chữ nhật có chiều dài 2/7 mét và chiều rộng 6/5 mét. Diện tích khu vườn là bao nhiêu.
Giải:
Diện tích của khu vườn đó là: 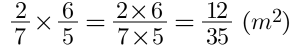
Cách khắc phục các lỗi thường gặp
– Lỗi 1: Quên rút gọn phân số
Đây là một lỗi khá phổ biến, đặc biệt là khi học sinh mới bắt đầu làm quen với phép nhân phân số. Nhiều học sinh sau khi nhân xong thường quên hoặc không biết cần rút gọn phân số. Kết quả chưa được rút gọn có thể bị trừ điểm hoặc gây khó khăn cho các phép tính tiếp theo.
Để tránh mắc phải lỗi sai cơ bản này, học sinh cần luôn kiểm tra lại đáp án sau khi đã thực hiện xong phép tính. Nếu tử số và mẫu số của kết quả có ước chung nào lớn hơn 1, người học cần thực hiện bước rút gọn phân số để đảm bảo kết quả chính xác nhất.

– Lỗi 2: Nhầm lẫn giữa tử số và mẫu số
Một lỗi khác mà học sinh mới đôi khi mắc phải là nhầm lẫn giữa tử số và mẫu số trong quá trình nhân. Thay vì nhân tử số với tử số và mẫu số với mẫu số, các bạn có thể nhầm lẫn với quy tắc của phép chia mà nhân tử số của phân số này với mẫu số của phân số kia.
Học sinh cần phải nắm vững khái niệm về các số trong cùng một phân số và các quy tắc khi thực hiện phép nhân để có thể tránh mắc phải sai sót này.
Kết luận
Thành thạo cách nhân hai phân số là bước đệm quan trọng giúp học sinh tiểu học nắm vững các giải các bài toán về phân số, biểu thức và bài toán thực tế. Hy vọng qua những chia sẻ trên của KidsUP, bạn đọc đã có thể thực hiện các bài toán nhân phân số một cách dễ dàng và nhanh chóng.













