Cách chứng minh hai đường thẳng song song là một trong những kiến thức cơ bản nhưng quan trọng trong chương trình Toán THCS. Không chỉ giúp học sinh hiểu rõ về hình học phẳng, mà còn rèn luyện kỹ năng tư duy logic, phân tích và suy luận. Bài viết dưới đây của KidsUP sẽ hướng dẫn bạn cách chứng minh hai đường thẳng song song một cách đơn giản và dễ hiểu nhất – chỉ với 3 bước!
Hiểu đúng về hai đường thẳng song song
Hai đường thẳng được gọi là song song khi chúng cùng nằm trong một mặt phẳng và không bao giờ cắt nhau, dù kéo dài vô hạn về hai phía. Trong hình học Euclid, khái niệm này là nền tảng để xây dựng các định lý liên quan đến góc, tam giác và hình học không gian.

Ví dụ quen thuộc về hai đường thẳng song song là hai cạnh đối diện của hình chữ nhật hoặc hai đường ray xe lửa chạy song song với nhau. Đặc điểm nổi bật của chúng là:
- Không có điểm chung.
- Có cùng phương (cùng độ nghiêng).
Việc hiểu rõ định nghĩa này sẽ là bước đệm giúp học sinh dễ dàng áp dụng vào việc chứng minh các bài toán liên quan đến đường thẳng song song.
3 dấu hiệu về hai đường thẳng song song
Trong chương trình Toán lớp 7, Bộ Giáo dục và Đào tạo đã đưa ra 3 dấu hiệu phổ biến để nhận biết hoặc chứng minh hai đường thẳng song song:
- Hai đường thẳng có một cặp góc so le trong bằng nhau → Hai đường đó song song.
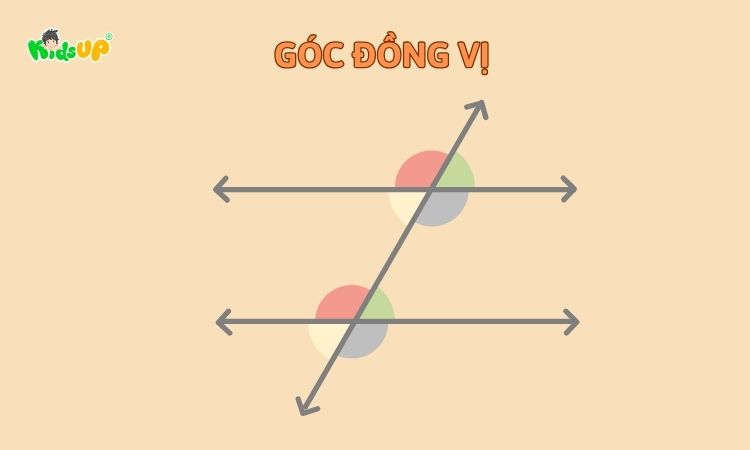
- Hai đường thẳng có một cặp góc đồng vị bằng nhau → Hai đường đó song song.
- Hai đường thẳng có một cặp góc trong cùng phía bù nhau (tổng bằng 180°) → Hai đường đó song song.
Những dấu hiệu này thường xuất hiện khi hai đường thẳng bị cắt bởi một đường thẳng thứ ba (gọi là đường cắt). Việc nhận diện đúng loại góc trong từng tình huống sẽ giúp học sinh dễ dàng lựa chọn phương pháp chứng minh phù hợp.
3 bước đơn giản để chứng minh hai đường thẳng song song
Để chứng minh hai đường thẳng song song, học sinh chỉ cần thực hiện theo đúng 3 bước sau. Bạn hãy làm theo từng bước để không bị thiếu dẫn chứng nhé.

Bước 1 – Xác định các cặp góc liên quan
Trong một hình vẽ có hai đường thẳng và một đường cắt, bước đầu tiên là quan sát và xác định các cặp góc có thể sử dụng. Tùy vào bài toán, bạn có thể thấy các cặp góc:
- So le trong
- Đồng vị
- Trong cùng phía
Việc xác định đúng góc là yếu tố then chốt quyết định hướng giải.
Bước 2 – Tính hoặc so sánh số đo các góc
Sau khi đã xác định được các cặp góc, học sinh cần:
- Sử dụng các tính chất của góc để tính giá trị cụ thể.
- Hoặc nếu đã có dữ liệu, hãy so sánh trực tiếp số đo giữa các góc liên quan.
Nếu phát hiện hai góc bằng nhau hoặc có tổng bằng 180°, đây sẽ là căn cứ để đưa ra kết luận.
Bước 3 – Áp dụng dấu hiệu nhận biết để kết luận
Dựa vào kết quả tính toán hoặc so sánh ở bước 2, bạn có thể áp dụng các dấu hiệu đã học để kết luận hai đường thẳng song song. Hãy viết kết luận thật rõ ràng, có căn cứ cụ thể từ bước trên để bài làm chặt chẽ và chính xác.
Ví dụ dễ hiểu về hai đường thẳng song song
Dưới đây là một số ví dụ minh họa thực tế để giúp bạn vận dụng hiệu quả kiến thức vừa học:
Ví dụ 1 – Sử dụng góc so le trong
Vẽ hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc tạo bởi a và c là 65°, góc so le trong phía b là 65°.
→ Vì hai góc so le trong bằng nhau nên suy ra a // b.
Ví dụ 2 – Sử dụng góc đồng vị
Cho đường thẳng a và b cắt bởi đường thẳng c. Biết góc đồng vị giữa a và c bằng 120°, góc tương ứng giữa b và c cũng là 120°.
→ Kết luận: a // b.
Ví dụ 3 – Sử dụng góc trong cùng phía bù nhau
Trong hình vẽ, hai góc trong cùng phía lần lượt là 110° và 70°.
→ Tổng = 180° → Hai đường thẳng song song.
Thực hành cách chứng minh hai đường thẳng song song
– Bài 1: Cho hình vẽ, xác định các cặp góc so le trong và chứng minh hai đường thẳng song song.
- Vẽ hai đường thẳng a, b cắt bởi c.
- Cho biết góc giữa a và c là 60°, xác định góc so le trong với góc này.
- Chứng minh a // b.
– Bài 2: Cho hình vẽ, xác định các cặp góc đồng vị và hai đường thẳng song song
- Trong hình, có 2 góc đồng vị lần lượt bằng 100°.
- Áp dụng dấu hiệu góc đồng vị để chứng minh.
– Bài 3: Cho hình vẽ, xác định các cặp góc trong cùng phía bù nhau và hai đường thẳng song song.
- Cho hai góc trong cùng phía là 80° và 100°.
- Tổng = 180° → Áp dụng dấu hiệu thứ ba để kết luận.
Kết luận
Chứng minh hai đường thẳng song song là kỹ năng quan trọng và thường xuyên xuất hiện trong các đề kiểm tra Toán học. Với 3 bước đơn giản cùng các ví dụ thực tế mà KidsUP cia sẻ ở trên, học sinh hoàn toàn có thể làm chủ được dạng bài này. Hãy luyện tập thật nhiều để rèn sự quan sát và tư duy logic.













